深度强化学习：从0到100教机器人操控无人机飞行（下）

三. 构建策略网络（Policy Network）

正如前文所述，我们将使用神经网络作为 “智能体的大脑”，即策略网络。换句话说，它的任务是根据当前环境的状态（state vector），输出一个动作的概率分布，告诉智能体下一步该怎么做。

下面是一个简单的实现：它接收状态向量作为输入，输出 3 个独立动作（对应三个推进器）的概率分布。

• 启动主推进器
• 启动左推进器
• 启动右推进器

def state_to_array(state):
    """Helper function to convert DroneState dataclass to numpy array"""
    data = np.array([
        state.drone_x,
        state.drone_y,
        state.drone_vx,
        state.drone_vy,
        state.drone_angle,
        state.drone_angular_vel,
        state.drone_fuel,
        state.platform_x,
        state.platform_y,
        state.distance_to_platform,
        state.dx_to_platform,
        state.dy_to_platform,
        state.speed,
        float(state.landed),
        float(state.crashed)
    ])
    
    return torch.tensor(data, dtype=torch.float32)

class DroneGamerBoi(nn.Module):
    def __init__(self, state_dim=15):
        super().__init__()
        
        self.network = nn.Sequential(
            nn.Linear(state_dim, 128),
            nn.LayerNorm(128),
            nn.ReLU(),
            nn.Linear(128, 128),
            nn.LayerNorm(128),
            nn.ReLU(),
            nn.Linear(128, 64),
            nn.LayerNorm(64),
            nn.ReLU(),
            nn.Linear(64, 3),
            nn.Sigmoid()
        )
        
    def forward(self, state):
        if isinstance(state, DroneState):
            state = state_to_array(state)
        
        return self.network(state)

实际上，我没有采用 “2³=8 种离散动作组合” 的方案（毕竟三个推进器，每个都可以“开”或“关”，理论上会形成 8 种动作可能）。相反，我把问题简化成了对三个独立推进器分别做决策，并使用 伯努利采样（Bernoulli sampling） 来决定是否激活每个推进器。这种简化让优化更简单 —— 因为每个推进器的决策是独立的，而不需要在一个大的类别里纠结哪个组合更好（至少我是这么认为的，可能不对，但确实有效！）。

 

四. 用策略梯度（Policy Gradient）训练策略

学习策略：何时更新网络？

我早期曾被一个问题困住：“到底是每执行一个动作就立刻更新一次策略，还是等整个 episode（完整的一轮任务）跑完之后，再统一更新？”事实证明，这个选择对训练效果影响巨大。

如果仅根据单个动作的奖励来优化策略，会导致 “高方差问题”—— 简单说，训练信号充满噪声，梯度方向混乱无章！所谓 “高方差”，是指优化算法在更新策略网络参数时，接收到的梯度信号相互矛盾：同样的动作，在略有不同的状态下，可能会得到完全相反的梯度方向。这会导致训练缓慢，甚至完全停滞。

我们有三种策略更新方式：

1. 每个动作更新（Per-Step Updates）

无人机启动一次推进器，获得少量奖励，然后立即更新整个策略。这就像每投一次篮球，就立刻调整投篮姿势 —— 反应过度了！一次 “运气好” 的动作（比如偶然获得更高奖励）不代表智能体做得对，一次 “运气差” 的动作也不代表做得错。此时的训练信号噪声太大。

我的第一次尝试：我早期用了这种方式，结果无人机只会随机乱晃，偶尔靠运气做出一个能多拿点奖励的动作，就立刻 “过拟合” 到这个动作上，之后反复尝试复现，却不断坠毁。那场景看得人难受 —— 就像看一个人从纯粹的巧合里学到错误的教训，一遍又一遍地重蹈覆辙。

2. 每回合更新（Per-Episode Updates）

这种方式好多了！让无人机完整尝试一次着陆（无论成功还是坠毁），看完整个过程后再更新策略。这就像打完一局游戏后，复盘思考需要改进的地方。至少现在我们能看到 “动作的完整后果” 了。但问题在于：如果这次着陆只是运气好（或运气差）呢？我们仍然只依赖 “单个数据点” 来学习。

3. 多次回合后批量更新（Multi-Episode Batch Updates）

这是最优方案。我们同时运行多次（我用了 6 次）无人机着陆尝试，看完所有尝试的结果后，根据 “平均表现” 更新策略。有些尝试可能运气好，有些可能运气差，但取平均值后，我们能更清楚地知道 “到底什么方法真的有效”。虽然这种方式对电脑算力要求较高，但只要能运行，效果远好于前两种。当然，这方法并非最优，但容易理解和实现 —— 还有其他更好的方法。

以下是在无人机游戏中收集多个回合的代码：

def collect_episodes(client: DroneGameClient, policy: nn.Module, max_steps=300):
    """
    Collect episodes with early stopping
    
    Args:
        client: The game's socket client
        policy: PyTorch module
        max_steps: Maximum steps per episode (default: 300)
    """
    num_games = client.num_games
    
    # Initialize storage
    all_episodes = [{'states': [], 'actions': [], 'log_probs': [], 'rewards': [], 'done': False} 
                    for _ in range(num_games)]
    
    # Reset all games
    game_states = [client.reset(game_id) for game_id in range(num_games)]
    step_counts = [0] * num_games  # Track steps per game
    
    while not all(ep['done'] for ep in all_episodes):
        # Batch active games
        batch_states = []
        active_game_ids = []
        
        for game_id in range(num_games):
            if not all_episodes[game_id]['done']:
                batch_states.append(state_to_array(game_states[game_id]))
                active_game_ids.append(game_id)
        
        if len(batch_states) == 0:
            break
        
        # Batched inference
        batch_states_tensor = torch.stack(batch_states)
        batch_action_probs = policy(batch_states_tensor)
        batch_dist = Bernoulli(probs=batch_action_probs)
        batch_actions = batch_dist.sample()
        batch_log_probs = batch_dist.log_prob(batch_actions).sum(dim=1)
        
        # Execute actions
        for i, game_id in enumerate(active_game_ids):
            action = batch_actions[i]
            log_prob = batch_log_probs[i]
            
            next_state, _, done, _ = client.step({
                "main_thrust": int(action[0]),
                "left_thrust": int(action[1]),
                "right_thrust": int(action[2])
            }, game_id)
            
            reward = calc_reward(next_state)
            
            # Store data
            all_episodes[game_id]['states'].append(batch_states[i])
            all_episodes[game_id]['actions'].append(action)
            all_episodes[game_id]['log_probs'].append(log_prob)
            all_episodes[game_id]['rewards'].append(reward['total'])
            
            # Update state and step count
            game_states[game_id] = next_state
            step_counts[game_id] += 1
            
            # Check done conditions
            if done or step_counts[game_id] >= max_steps:
                # Apply timeout penalty if hit max steps without landing
                if step_counts[game_id] >= max_steps and not next_state.landed:
                    all_episodes[game_id]['rewards'][-1] -= 500  # Timeout penalty
                
                all_episodes[game_id]['done'] = True
    
    # Return episodes
    return [(ep['states'], ep['actions'], ep['log_probs'], ep['rewards']) 
            for ep in all_episodes]

最大化与最小化的难题

在传统深度学习（监督学习）中，我们的目标是 最小化损失函数：

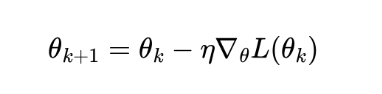
我们希望沿着梯度方向“下山”，让损失越来越小（预测越来越准）。

但在强化学习中，我们的目标是 “最大化总奖励”！核心目标是：

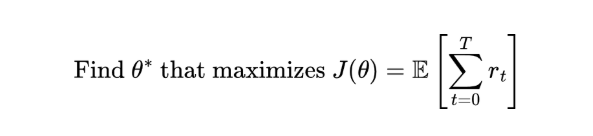
问题来了：现有的深度学习框架（如 PyTorch、TensorFlow）是为 “最小化” 设计的，不是为 “最大化” 设计的。那么，怎么把 “最大化奖励” 转换成 “最小化损失” 呢？

简单技巧：最大化 J(θ) 等价于最小化它的相反数（即 J (θ) 的负值），Maximize J(θ)=Minimize −J(θ)

因此，我们的损失函数变成了：

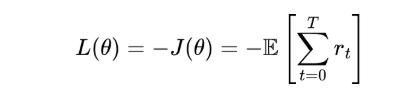
这样一来，梯度下降（gradient descent） 实际上就会在“奖励地形”上向上爬坡（更像是“梯度上升”）。 因为我们是在最小化“负奖励”，等价于最大化“正奖励”。

REINFORCE 算法（策略梯度的经典实现）

策略梯度定理（Policy Gradient Theorem, Williams, 1992）告诉我们如何计算 “期望奖励” 的梯度：

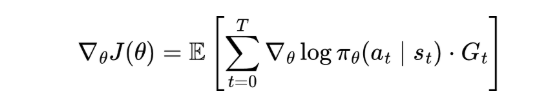
（我知道这公式看起来吓人，但只要理解核心逻辑，就会发现它其实很简洁！）

其中：

• πθ​(at​∣st​)：目标函数 J (θ) 对网络参数 θ 的梯度（即 “该往哪个方向调整参数，才能让奖励更高”）
• E […]：期望（可以理解为 “平均”）
• logπθ(at|st)：在状态 st 下，策略 πθ 选择动作 at 的对数概率
• Gt：从时间步 t 开始的总折扣回报（即 “动作 at 带来的后续总奖励”）

用大白话解释（因为公式太密集）：

1. 如果动作 at 带来了高回报 Gt（后续总奖励高），就提高这个动作的概率；
2. 如果动作 at 带来了低回报 Gt（后续总奖励低），就降低这个动作的概率；
3. 梯度告诉我们 “该调整神经网络的权重” 的方向。

引入基准值（Baseline）：减少方差

直接使用原始回报 Gt 会导致 “高方差”（梯度噪声大）。我们可以通过引入一个基线函数 b(st ) 来改善这一问题：

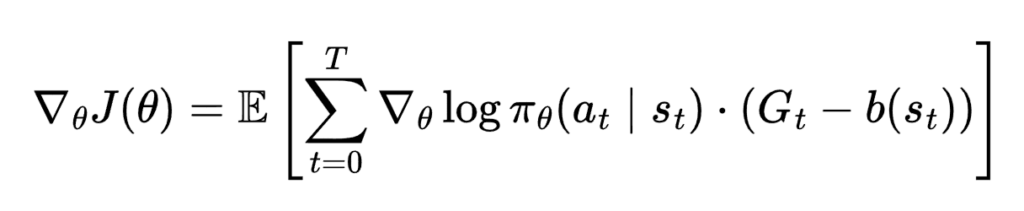
最简单的基准值，就是 平均回报（mean return）：

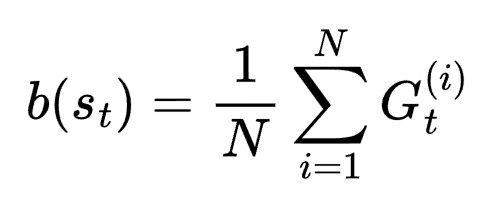
这就得到了 “优势值”（Advantage）：At = Gt – b

• 优势值为正 → 该动作比平均水平好 → 提高概率；
• 优势值为负 → 该动作比平均水平差 → 降低概率。

为什么这有用？举个例子：与其说 “这个动作得了 100 分”（100 分算好吗？），不如说 “这个动作得了 100 分，而平均只有 50 分”（这就明确是“很好”了）。相对表现比绝对分数更清晰。

我们的实现（带基准值的 REINFORCE 算法）

在无人机着陆代码中，我们用了带基准值的 REINFORCE 算法：

# 1. Collect episodes and compute returns
returns = compute_returns(rewards, gamma=0.99)  # G_t with discounting

# 2. Compute baseline (mean of all returns)
baseline = returns_tensor.mean()

# 3. Compute advantages
advantages = returns_tensor - baseline

# 4. Normalize advantages (extra variance reduction)
advantages = (advantages - advantages.mean()) / (advantages.std() + 1e-8)

# 5. Compute loss (note the negative sign!)
loss = -(log_probs_tensor * advantages).mean()

# 6. Gradient descent
optimizer.zero_grad()
loss.backward()
optimizer.step()

我们会重复上述循环，直到无人机学会正确着陆（或达到预设的训练次数）。想看完整代码实现，可以查看对应的 notebook 示例！

 

五. 当前结果（奖励函数缺陷改进）

经过无数小时的奖励函数调整、超参数优化，以及看着无人机以各种 “奇葩方式” 坠毁后，我终于让它 “基本能用” 了！虽然我设计的奖励函数并不完美，但它确实能教会策略网络如何让无人机安全着陆。以下是一次成功的着陆示例：

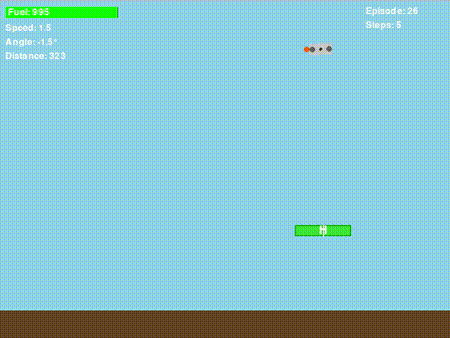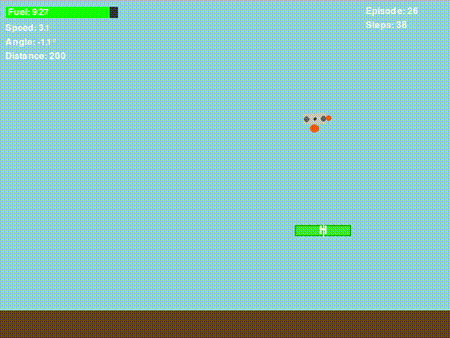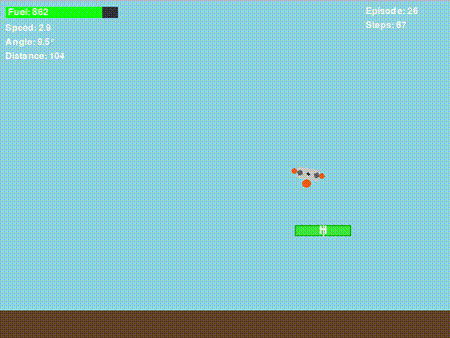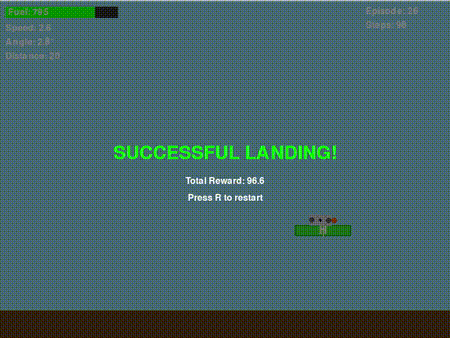
很酷，对吧？但接下来的情况既有趣又让人沮丧……

顽固的悬停问题：一个根本性局限

即便我改进了奖励函数，加入了 “垂直位置条件”（只有 drone_y > platform_y，即无人机在平台上方时才给正奖励），训练后的策略仍有一个让人头疼的行为：当无人机错过平台时，它会朝着平台下降，但到了平台下方后，就会悬停不动，不再尝试着陆。

我花了一周多时间盯着奖励曲线（还不断修改奖励函数），疑惑为什么 “修复后的” 奖励函数还会导致这种悬停行为。直到我画出 “累积奖励曲线”，才看清了规律 —— 说实话，我都没法怪智能体找到这个策略。

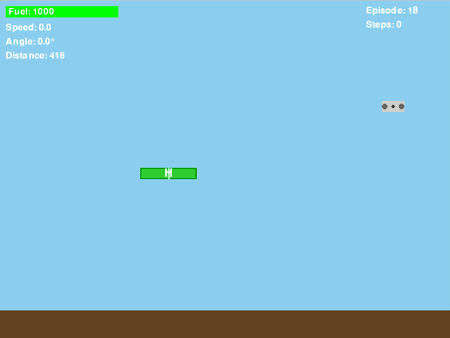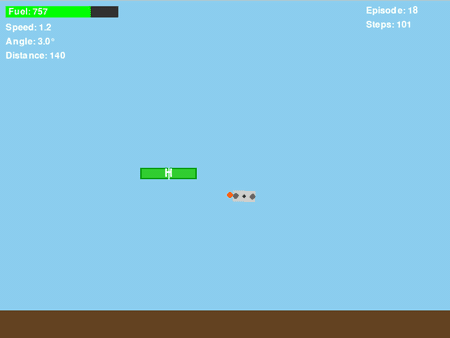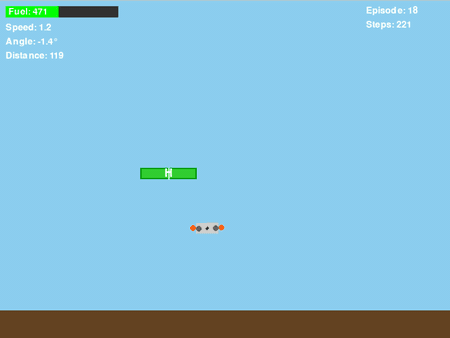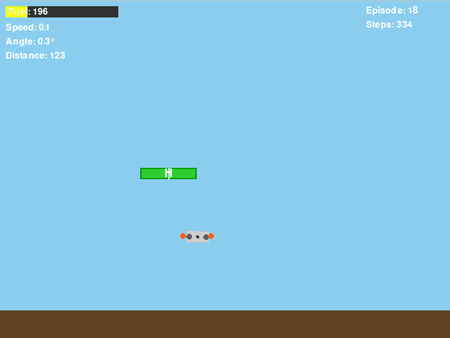
图 7：动图展示了“在平台下方悬停”的问题

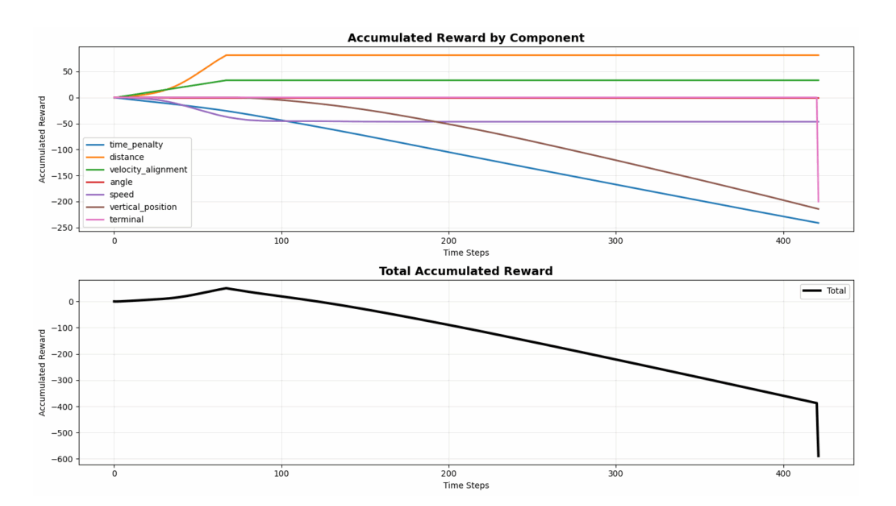
图 8：曲线显示无人机明显在进行奖励漏洞利用

图表揭示的规律如下：

• 距离奖励（橙色）：前期累积到约 + 70，之后进入平台期（不再获得奖励）
• 速度对齐奖励（绿色）：前期累积到约 + 30，之后进入平台期
• 时间惩罚（蓝色）：稳步累积到约 – 250（惩罚持续增加）
• 垂直位置惩罚（棕色）：稳步累积到约 – 200（因处于平台下方而产生的惩罚）
• 总奖励：超时后最终在 – 400 至 – 600 之间

核心结论：无人机从平台上方开始下降（下降过程中累积距离和速度奖励），经过平台高度后，并未完成着陆，而是在平台下方悬停。一旦处于平台下方，它就不再获得正奖励（注意距离和速度奖励曲线在约 50-60 步时进入平台期），但会持续累积时间惩罚和垂直位置惩罚。即便如此，这种策略依然 “可行”—— 因为尝试着陆可能面临立即 – 200 的坠毁惩罚，而在下方悬停 “仅” 会在整个回合结束时累积约 – 400 至 – 600 的惩罚（两害相权取其轻）。

为何会出现这种情况？

根本问题在于，我们的奖励函数 r (s’, a) 只能 “看到当前状态”，无法 “理解整个轨迹”（即动作序列和状态变化过程）。试想：在任意单个时间步，奖励函数无法区分以下两种情况：

1. 无人机在向着陆目标推进（从上方受控下降，逐步靠近平台）
2. 无人机在利用奖励规则漏洞（通过来回晃动骗取奖励）

这两种情况在某个时刻可能拥有相同的 dy_to_platform > 0（无人机在平台上方）状态，因此会获得完全相同的奖励！智能体并不 “笨”—— 它只是在严格执行你设定的优化目标（最大化奖励）而已。

如何真正解决这个问题？

要彻底解决该问题，我个人认为，奖励不应只依赖当前状态 r (s, a)，而应依赖 “状态转移” r (s, a, s’)（s 为当前状态，s’ 为执行动作后的下一状态）。这样就能基于以下维度设计奖励规则：

• 进度奖励：仅当 distance (s’) < distance (s)（无人机确实在靠近平台）时，才给予奖励
• 垂直改进奖励：仅当无人机相对平台持续向上移动（逐步调整到着陆高度）时，才给予奖励
• 轨迹一致性惩罚：对表明 “来回晃动” 的快速方向变化施加惩罚

这是一种更具原则性的解决方案，而非通过不断加重惩罚来 “修补” 奖励函数（我之前尝试过用各种惩罚去修补漏洞，但效果并不好）。作弊行为之所以存在，本质上是因为我们的奖励函数缺少 “轨迹信息”。

在下一篇文章中，我将探讨 Actor-Critic 方法，以及能融入时间序列信息的技术，从而防止这类作弊策略。敬请关注！

如果您找到了解决此问题的方法，欢迎与我联系！

至此，《深度强化学习入门：从 0 到 1》这篇文章就结束了

 

作者：Vedant Jumle

原文链接：https://towardsdatascience.com/deep-reinforcement-learning-for-dummies/