用机器学习预测股票价格

股市以波动性强、动态性高、非线性著称。要精确预测股价极具挑战，因为它受多种宏观与微观因素影响：政治、全球经济状况、突发事件、公司的财务表现等等。

但这也意味着：数据很多，可挖的模式也不少。因此，金融分析师、研究人员与数据科学家不断尝试用各种分析技术捕捉市场趋势。这也催生了算法交易的概念：用自动化、预先编程的交易策略来执行下单。

在本文中，我们将结合传统量化金融方法与机器学习算法来预测股价走势，主要涵盖以下主题：

• 股票分析：基本面 vs 技术面
• 把股价当作时间序列数据及相关概念
• 利用移动平均（Moving Average）技术预测股价
• LSTM 简介
• 用 LSTM 模型预测股价
• 对新方法（比如 ESN）的思考与展望

免责声明：本文/项目不提供任何金融、交易或投资建议；作者不对模型的准确性作出任何保证。若读者希望依据文中方法或代码进行投资决策，请务必自行进行充分尽调。

 

一. 股票分析：基本面 vs 技术面

当谈到股票分析，基本面分析与技术面分析往往位于市场分析光谱的两端。

基本面分析（Fundamental Analysis）

• 通过研究公司的内在价值（intrinsic value）来评估股票，包括但不限于有形资产、财务报表、管理层绩效、战略举措以及消费者行为——在本质上是公司的“底子”。
• 作为长期投资的重要指标，基本面分析依赖历史数据与当前数据来衡量收入、资产、成本与负债等关键指标。
• 一般而言，基本面结论不会因短期新闻而大幅改变。

技术面分析（technical analysis）

• 研究来自股市活动的可量化数据，例如股价、历史收益、交易量等，也就是那些能帮助识别交易信号、捕捉市场运动模式的统计信息。
• 与基本面分析一样，它同样利用历史与当前数据，但主要用于短线/中短线交易。
• 由于其短期特性，技术分析结果更容易受到新闻或市场情绪波动影响。
• 常见技术分析方法包括：移动平均（Moving Average, MA）、支撑与阻力位、以及趋势线与价格通道（trend lines & channels）。

在本文的实操部分，我们将只关注技术分析（technical analysis），重点使用两种经典方法来预测股价：

• 简单移动平均（Simple Moving Average，SMA）
• 指数移动平均（Exponential Moving Average，EMA）

同时，我们还将引入一种针对时间序列的深度学习框架 —— LSTM（长短期记忆网络，Long Short-Term Memory），以此构建预测模型，并将其表现与上述技术分析方法进行对比。

依照免责声明，本文并不涉及任何股票交易策略。文中提到的投资或交易术语，仅用于帮助理解分析过程，不构成投资建议。

在文中你会看到一些术语，例如：

• 趋势指标：表征股价趋势的统计量；
• 中期走势：如常见的 50 日价格运动趋势。

 

二. 把股价当作时间序列数据及相关概念

尽管股价波动剧烈，但它们并不是随机生成的数字。它可以被看作一串离散时间数据（discrete-time data）：就是在连续时间点上（通常以日频为单位）观测到的数值。时间序列预测（用历史值预测未来值）非常适用于股价预测。

鉴于时间序列具有“顺序性”，我们需要某种方式来聚合这串信息。在众多技术中，最直观的是 移动平均（MA）：它能平滑短期波动，使整体趋势更清晰。

 

三. 数据集分析

本次演示，我们将使用 Apple（AAPL） 过去 21 年（1999-11-01 到 2021-07-09）的收盘价作为研究对象，数据来自 Alpha Vantage（提供免费历史/实时行情 API）。

使用 Alpha Vantage 需要一个免费 API Key。如果不想创建 API，也可直接使用本文准备好的数据；若想换其他股票，下载代码在本文配套的 GitHub 仓库里。拿到 API 后，只需提供股票的 ticker。

在模型训练部分，我们将使用最早的 80% 数据作为训练集， 并将最近的 20% 数据保留为测试集。

# %% Train-Test split for time-series
stockprices = pd.read_csv("stock_market_data-AAPL.csv", index_col="Date")

test_ratio = 0.2
training_ratio = 1 - test_ratio

train_size = int(training_ratio * len(stockprices))
test_size = int(test_ratio * len(stockprices))
print(f"train_size: {train_size}")
print(f"test_size: {test_size}")

train = stockprices[:train_size][["Close"]]
test = stockprices[train_size:][["Close"]]

 

四. 创建项目

在模型训练和性能比较方面，neptune.ai 使用户能够方便地跟踪所有与模型相关的内容，包括超参数规范和评估图表。

现在，让我们在 Neptune 中创建一个项目来进行这项练习，并将其命名为“StockPrediction”。

 

五. 评估指标与辅助函数

股价预测本质是一个回归问题，我们采用 RMSE（均方根误差） 与 MAPE（平均绝对百分比误差，%） 作为模型的评估指标，这两个指标都是衡量预测准确度的常用方法。

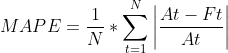
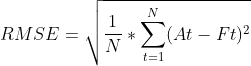
N 表示时间点的数量； 𝐴 𝑡 为真实股价（actual / true stock price）； 𝐹 𝑡 为预测股价（predicted / forecast value）

RMSE 衡量的是预测值与真实值之间的绝对差异，MAPE (%) 衡量该差值相对真实值的百分比（例如 MAPE=12%，表示预测股价与真实股价的平均相对误差为 12%）。

接下来，我们将为本次实验编写几个辅助函数（helper functions）。

1）将股价拆成训练序列 X（输入） 与下一时刻的输出值 Y（目标）。

## Split the time-series data into training seq X and output value Y
def extract_seqX_outcomeY(data, N, offset):
    """
    Split time-series into training sequence X and outcome value Y
    Args:
        data - dataset
        N - window size, e.g., 50 for 50 days of historical stock prices
        offset - position to start the split
    """
    X, y = [], []

    for i in range(offset, len(data)):
        X.append(data[i - N : i])
        y.append(data[i])

    return np.array(X), np.array(y)

2）计算 RMSE（均方根误差） 和 MAPE（平均绝对百分比误差 %）。

#### Calculate the metrics RMSE and MAPE ####
def calculate_rmse(y_true, y_pred):
"""
Calculate the Root Mean Squared Error (RMSE)
"""
rmse = np.sqrt(np.mean((y_true - y_pred) ** 2))
return rmse

def calculate_mape(y_true, y_pred):
"""
Calculate the Mean Absolute Percentage Error (MAPE) %
"""
y_pred, y_true = np.array(y_pred), np.array(y_true)
mape = np.mean(np.abs((y_true - y_pred) / y_true)) * 100
return mape

3）计算技术分析模型的评估指标（RMSE 与 MAPE），并将结果记录到 Neptune 中。

def calculate_perf_metrics(var):
### RMSE
rmse = calculate_rmse(
np.array(stockprices[train_size:]["Close"]),
np.array(stockprices[train_size:][var]),
)
### MAPE
mape = calculate_mape(
np.array(stockprices[train_size:]["Close"]),
np.array(stockprices[train_size:][var]),
)

## Log to Neptune
run["RMSE"] = rmse
run["MAPE (%)"] = mape

return rmse, mape

4）绘制股价趋势并上传到 Neptune。

def plot_stock_trend(var, cur_title, stockprices=stockprices):
ax = stockprices[["Close", var, "200day"]].plot(figsize=(20, 10))
plt.grid(False)
plt.title(cur_title)
plt.axis("tight")
plt.ylabel("Stock Price ($)")

## Log to Neptune
run["Plot of Stock Predictions"].upload(
neptune.types.File.as_image(ax.get_figure())
)

 

六. 使用移动平均（MA）技术预测股价

移动平均（Moving Average, MA） 是一种常用的方法，用于平滑股市中的随机波动。 它的原理类似一个滑动窗口：在时间序列上不断前移，每次取一段时间内的数据求平均， 新的数据点加入时，旧的数据点会被移除。

常用的MA周期包括：20 日均线（短期）、50 日均线（中期）、200 日均线（长期）。

在众多移动平均方法中，分析师最常使用的两种是：简单移动平均（Simple Moving Average, SMA）和 指数移动平均（Exponential Moving Average, EMA）

简单移动平均（SMA）

SMA是指在给定时间窗口内，对一段时期的股票（通常为收盘价）求取算术平均值。

P n ​ 表示第n 个时间点的股票价格，N 表示时间窗口内的数据点数量。

在本次 SMA 模型的练习中，我们将使用下面的 Python 代码来计算 50 日简单移动平均（SMA）， 并额外加入一个 200 日 SMA 作为参考对照。

window_size = 50

# Initialize a Neptune run
run = neptune.init_run(
project=myProject,
name="SMA",
description="stock-prediction-machine-learning",
tags=["stockprediction", "MA_Simple", "neptune"],
)

window_var = f"{window_size}day"

stockprices[window_var] = stockprices["Close"].rolling(window_size).mean()

### Include a 200-day SMA for reference
stockprices["200day"] = stockprices["Close"].rolling(200).mean()

### Plot and performance metrics for SMA model
plot_stock_trend(var=window_var, cur_title="Simple Moving Averages")
rmse_sma, mape_sma = calculate_perf_metrics(var=window_var)

### Stop the run
run.stop()

在 Neptune 的这次运行中，我们可以看到模型在测试集上的性能指标：RMSE = 43.77，MAPE = 12.53%。趋势图也能直观看到 50 日/200 日 的预测与真实收盘价的对比。

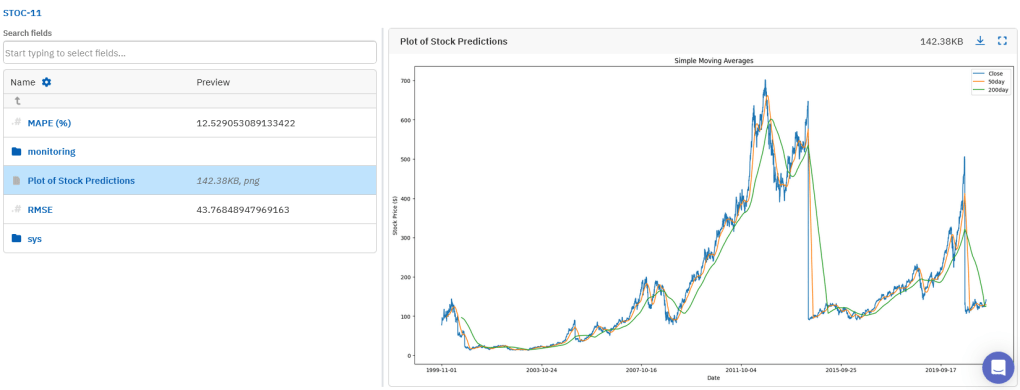
可以看出，在短期到中期走势上，50 日 SMA 比 200 日 SMA 更灵敏。不过，两种指标整体上都略低估了实际股价。

指数移动平均（EMA）

不同于 SMA，EMA 会对近期价格赋予更高权重，在我们的示例中，50 日均线的尾部数据点将被赋予更大的影响力。权重系数的大小取决于所选的时间周期数。其计算公式为：

• P t ​ ：第  t 个时间点的价格；
• EMA t−1 ​ ：上一个时间点的 EMA 值；
• N：EMA 的时间周期数；
• 权重系数  k = 2/(N+1) ​ 。

相较于 SMA，EMA 的优势在于它对价格变化更敏感， 因此更适合短期交易场景。 下面是一个 EMA 的 Python 实现示例：

# Initialize a Neptune run
run = neptune.init_run(
project=myProject,
name="EMA",
description="stock-prediction-machine-learning",
tags=["stockprediction", "MA_Exponential", "neptune"],
)

###### Exponential MA
window_ema_var = f"{window_var}_EMA"

# Calculate the 50-day exponentially weighted moving average
stockprices[window_ema_var] = (
stockprices["Close"].ewm(span=window_size, adjust=False).mean()
)
stockprices["200day"] = stockprices["Close"].rolling(200).mean()

### Plot and performance metrics for EMA model
plot_stock_trend(
var=window_ema_var, cur_title="Exponential Moving Averages")
rmse_ema, mape_ema = calculate_perf_metrics(var=window_ema_var)

### Stop the run
run.stop()

从 Neptune 记录的指标看：RMSE = 36.68、MAPE = 10.71%，相比 SMA（43.77 / 12.53%） 有明显提升。趋势图也显示 EMA 的表现优于 SMA。

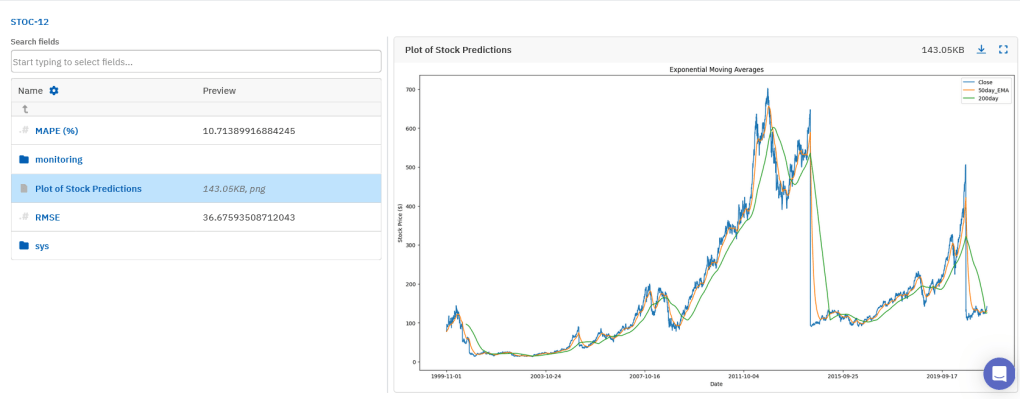
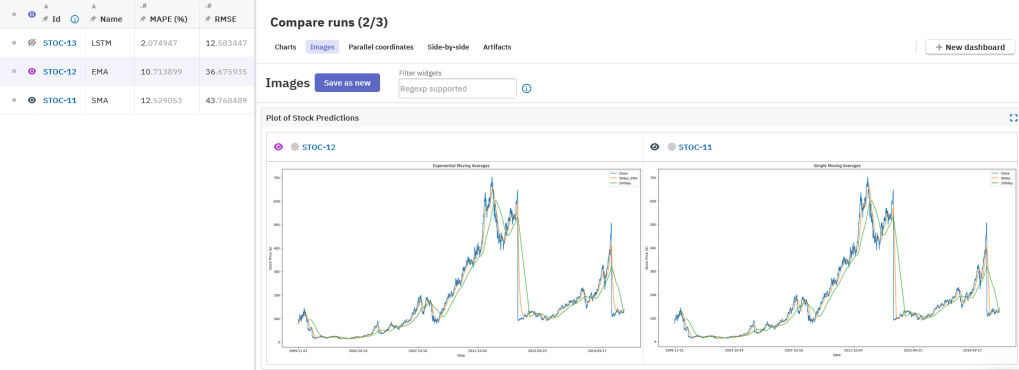
SMA vs EMA 对比

下方截图展示了 SMA 与 EMA 在 Neptune 中的并列对比结果。

七. LSTM 简介

接下来进入 LSTM。LSTM（Long Short-Term Memory）是处理时间序列的强力算法，它能捕捉历史模式，对未来数值做出较高精度预测。

简而言之，理解 LSTM 模型 的关键在于它的核心组件——单元状态（Cell State，记作C t ​ ）。 它代表了神经元内部同时存在的短期记忆与长期记忆。

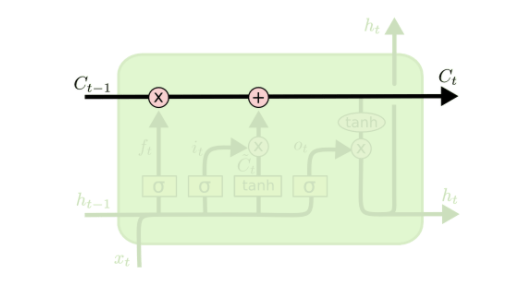
为了控制和管理单元状态（Cell State），LSTM 模型内部包含三个“门”（gates）或层。这里的“门”可以理解为一种信息过滤器：决定哪些信息被记住（让它通过），哪些被遗忘（过滤掉）。

遗忘门（Forget gate）

顾名思义，遗忘门决定了当前单元状态中哪些信息需要被丢弃。𝜎 表示 sigmoid 函数，它会对前一时刻的隐藏状态 ℎ 𝑡 − 1 与当前输入 𝑥 𝑡  进行加权计算，输出一个介于 [0, 1] 之间的值。1 表示“完全保留”，0 表示“完全过滤”。

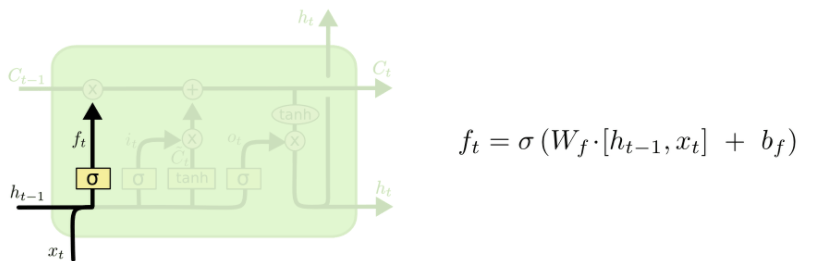
输入门（Input gate）

它用于决定哪些新的信息会被加入并存储到当前单元状态中。 在这一层中，首先使用 sigmoid 函数 处理输入向量 𝑖 𝑡 ​ ，以筛选出需要更新的信息；随后通过 tanh 函数 将候选状态 𝐶 𝑡 的取值压缩到区间 [-1, 1]。最后，将𝑖𝑡 与𝐶𝑡 ​逐元素相乘（即矩阵按元素相乘），得到需要写入当前单元状态的新信息。

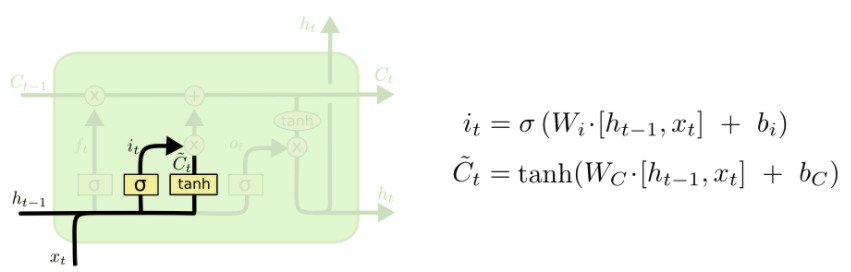
输出门（Output gate）

用于控制流向下一单元状态的信息输出。 它的工作方式与输入门类似：先通过 sigmoid 函数 筛选要输出的部分， 再使用 tanh 函数 对信息进行缩放，以过滤掉无关内容， 最终只保留我们希望传递出去的有效信息。

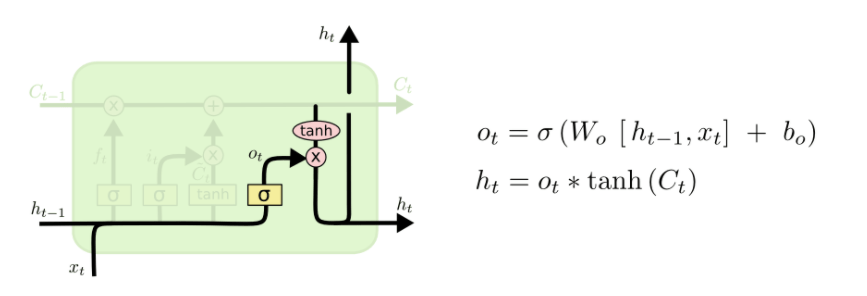
了解了 LSTM 的原理后，你可能已经开始好奇： 它在真实股价预测中表现如何？ 在接下来的部分，我们将构建一个 LSTM 模型， 并将其预测结果与SMA、 EMA进行对比。

 

八. 使用 LSTM 模型预测股价

首先，我们需要为 LSTM 模型 创建一个专属的 Neptune 实验， 并在其中设置好相关的超参数（hyper-parameters）

layer_units = 50
optimizer = "adam"
cur_epochs = 15
cur_batch_size = 20

cur_LSTM_args = {
"units": layer_units,
"optimizer": optimizer,
"batch_size": cur_batch_size,
"epochs": cur_epochs,
}

# Initialize a Neptune run
run = neptune.init_run(
project=myProject,
name="LSTM",
description="stock-prediction-machine-learning",
tags=["stockprediction", "LSTM", "neptune"],
)
run["LSTM_args"] = cur_LSTM_args

接着，我们需要对输入数据进行标准化处理（scaling），以便模型更好地收敛，然后将其划分为训练集和测试集。

# Scale our dataset
scaler = StandardScaler()
scaled_data = scaler.fit_transform(stockprices[["Close"]])
scaled_data_train = scaled_data[: train.shape[0]]

# We use past 50 days’ stock prices to predict the 51th day's closing price.
X_train, y_train = extract_seqX_outcomeY(scaled_data_train, window_size, window_size)

说明：

• 我们用 StandardScaler，而不是常见的 MinMaxScaler。原因在于股价是持续变化的，没有固定的最小值或最大值。 因此使用 MinMaxScaler 并不合理（虽然它一般也不会让模型崩溃）.
• 原始股价不能直接喂给 LSTM，需要用上面定义的 extract_seqX_outcomeY 做序列化。例如，为了预测第 51 天 的价格，该函数会使用前 50 天 的价格序列作为输入向量， 并将第 51 天的价格作为对应的输出标签。

接下来，我们开始 LSTM 模型的搭建与训练。我们将搭建一个包含两层隐藏层的 LSTM 网络， 并在输出层使用 线性（linear）激活函数。 同时，Neptune-Keras 集成记录训练过程。

### Setup Neptune's Keras integration ###
from neptune.integrations.tensorflow_keras import NeptuneCallback

neptune_callback = NeptuneCallback(run=run)

### Build a LSTM model and log training progress to Neptune ###
def Run_LSTM(X_train, layer_units=50):
inp = Input(shape=(X_train.shape[1], 1))

x = LSTM(units=layer_units, return_sequences=True)(inp)
x = LSTM(units=layer_units)(x)
out = Dense(1, activation="linear")(x)
model = Model(inp, out)

# Compile the LSTM neural net
model.compile(loss="mean_squared_error", optimizer="adam")

return model

model = Run_LSTM(X_train, layer_units=layer_units)

history = model.fit(
X_train,
y_train,
epochs=cur_epochs,
batch_size=cur_batch_size,
verbose=1,
validation_split=0.1,
shuffle=True,
callbacks=[neptune_callback],
)

训练过程可在 Neptune 中实时可视化。

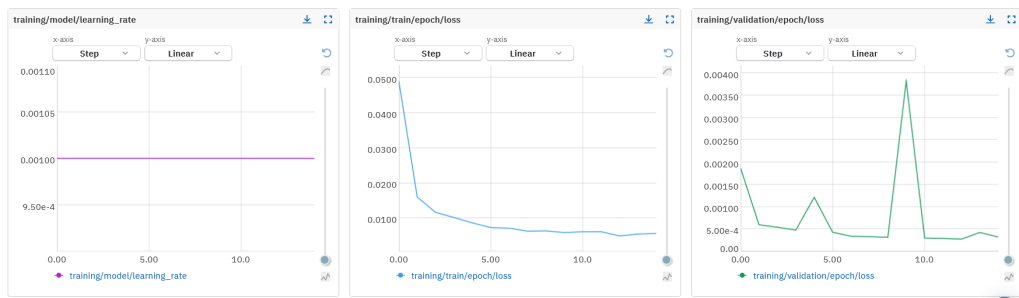
当模型训练完成后，我们将使用保留测试集（hold-out set）对其进行测试与验证

# predict stock prices using past window_size stock prices
def preprocess_testdat(data=stockprices, scaler=scaler, window_size=window_size, test=test):
raw = data["Close"][len(data) - len(test) - window_size:].values
raw = raw.reshape(-1,1)
raw = scaler.transform(raw)

X_test = [raw[i-window_size:i, 0] for i in range(window_size, raw.shape[0])]
X_test = np.array(X_test)

X_test = np.reshape(X_test, (X_test.shape[0], X_test.shape[1], 1))
return X_test

X_test = preprocess_testdat()
predicted_price_ = model.predict(X_test)
predicted_price = scaler.inverse_transform(predicted_price_)

# Plot predicted price vs actual closing price
test["Predictions_lstm"] = predicted_price

计算指标并记录到 Neptune，顺便画图：

# Evaluate performance
rmse_lstm = calculate_rmse(np.array(test["Close"]), np.array(test["Predictions_lstm"]))
mape_lstm = calculate_mape(np.array(test["Close"]), np.array(test["Predictions_lstm"]))

### Log to Neptune
run["RMSE"] = rmse_lstm
run["MAPE (%)"] = mape_lstm

### Plot prediction and true trends and log to Neptune
def plot_stock_trend_lstm(train, test):
fig = plt.figure(figsize = (20,10))
plt.plot(np.asarray(train.index), np.asarray(train["Close"]), label = "Train Closing Price")
plt.plot(np.asarray(test.index), np.asarray(test["Close"]), label = "Test Closing Price")
plt.plot(np.asarray(test.index), np.asarray(test["Predictions_lstm"]), label = "Predicted Closing Price")
plt.title("LSTM Model")
plt.xlabel("Date")
plt.ylabel("Stock Price ($)")
plt.legend(loc="upper left")

## Log image to Neptune
run["Plot of Stock Predictions"].upload(neptune.types.File.as_image(fig))

plot_stock_trend_lstm(train, test)

### Stop the run after logging
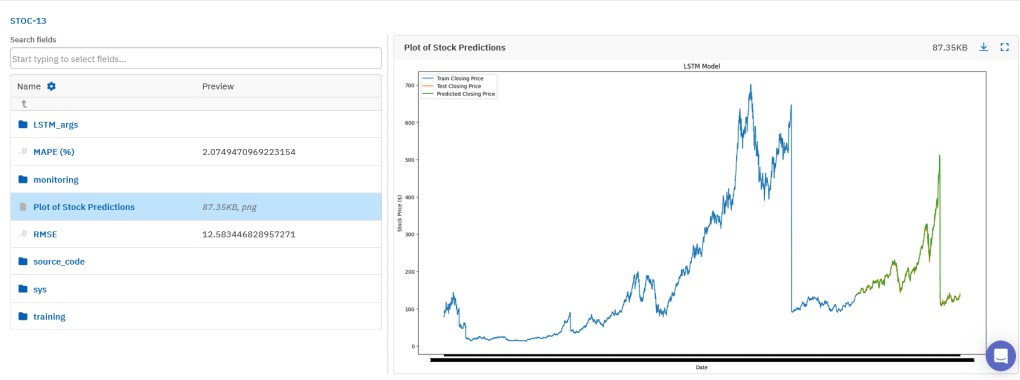
run.stop()

在 Neptune 中可以看到：LSTM 模型 RMSE = 12.58，MAPE = 2%，相较 SMA/EMA 大幅提升。从趋势图来看，预测曲线与实际收盘价几乎完美重合，在测试集上呈现出极高的一致性。

九. 关于新方法的思考

通过苹果股价的预测案例，我们已经看到 LSTM 相比传统 移动平均（MA） 模型的明显优势。 但需要谨慎的是：这种结论不应轻易泛化到其他股票。 与多数平稳时间序列不同，股市数据几乎没有季节性，且往往高度混沌。

就本例而言，Apple 作为科技巨头之一，既有成熟的商业模式与管理，又经常受新品或新服务发布提振销售，这些因素降低了苹果股价的隐含波动率，使得 LSTM 相对更“容易”预测。换成高波动股票，难度会上升，这是常识但值得再次强调。

考虑股市的混沌动力学，人们提出了 Echo State Networks（ESN，回声状态网络）。ESN 作为 循环神经网络（RNN） 家族的新成员，它在隐藏层（被称为“水库”，reservoir）中引入了多个相互稀疏连接的流动神经元（neurons）， 用来捕捉输入数据的非线性历史信息。

从高层视角来看：ESN 把时间序列输入映射到一个高维特征空间（即动态水库），输出层再用线性激活函数给出最终预测。

此外，还有一些值得探索的方向，例如，将新闻与社交媒体的情绪分析（sentiment analysis）融入股市预测，以反映市场情绪对股价的短期影响。另一个方向是混合模型：把 MA 的预测值作为额外输入喂给 LSTM。还可以探索更多变体与组合，这里就不一一展开了。

希望你阅读这篇文章时能像我写它时一样愉快！

 

原文作者：Katherine (Yi) Li

原文链接：https://neptune.ai/blog/predicting-stock-prices-using-machine-learning